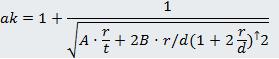
Formzahl αk
Die Formzahl αk ist ein auf der Geometrie beruhender Faktor für die Spannungserhöhung aufgrund von Kerben. Sie ist abhängig von der Belastungsart (Zug, Biegung, Torsion) und abhängig von der Geometrie, aber unabhängig vom Werkstoff.
Die Auswirkung auf das Bauteil wird über die Kerbwirkungszahl βk beschrieben. βk = αk / n mit n als Stützziffer.
Die Stützziffer n liegt zwischen 1 und αk , bei sehr zähen Materialien wird der Kerbgrund so plastifiziert, das die Kerbspannung gleich der Nennspannung ist (n = αk , βk = 1), bei sehr spröden Werkstoffen wirkt sich die Spannungserhöhung komplett aus ( n = 1, βk= αk )
Für αk gibt es Tabellen bzw. eben Berechnungen.
Für die Berechnungen habe ich folgende Formel übernommen:
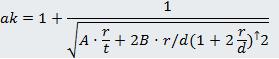
Quelle: siehe unten
Formzahl eines gekerbten Rundstabes mit Durchmesser D und Kerbradius r (umlaufende Rundnut) bei Zugbelastung
A=0.22, B=1.37
Formzahl eines Rundstabes mit Durchmesser D mit Absatz auf Durchmesser d und Radius am Absatz von r bei Zugbelastung
A=0.62, B=3.5
Quelle für Berechnung: